Question

h is a trigonometric function of the form h(x)=a sin(bx+c)+d. Below is the graph h(x). The function intersects its midline at (-pi,-8) and has a maximum point at (pi/4, "-1.5)." Find a formula for h(x). Give an exact expression.

Answer 1

6.5sin(.04x+.4pi)-8

Answer 2

The formula for h(x) is
`6.5 \sin \left( 0.2\pi x + (4\pi)/(5) \right) - 3`.

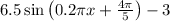The formula for the general sine function:

`y = A \sin \left( (2\pi)/(T) \left( x - h \right) \right) + d`

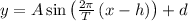
where:

A is the amplitude

T is the period

h is the horizontal shift

d is the vertical shift

In this case, the formula for h(x) is:

`h(x) = 10.5 \sin \left( (2\pi)/(10) \left( x - 2.5 \right) \right) - 3`

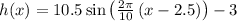
To simplify the expression, we can write:

`h(x) = 10.5 \sin \left( 0.2\pi x - 0.5\pi \right) - 3`

We can also write:

`h(x) = 6.5 \sin \left( 0.2\pi x + (4\pi)/(5) \right) - 3`