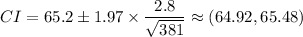Answer:
(64.92, 65.48)
Explanation:
The given details are;
The number of adults in the survey, n = 381 adults
The mean height of the adults in the survey,
 = 65.2 inches
= 65.2 inches
The standard deviation of the height of the adults in the survey, s = 2.8 inches
The confidence interval is given as follows;
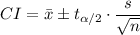
The test statistic for a 95% confidence interval with α = 0.05, the degrees of freedom, df = n-1 = 381 - 1 = 380,
 =
=
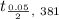 = 1.97
= 1.97
Therefore, we get;
C.I =