Question

To calculate the volume of a chemical produced in a day a chemical manufacturing company uses the following formula below:


`V(x)=[C_1(x)+C_2(x)](H(x))`
where represents the number of units produced. This means two chemicals are added together to make a new chemical and the resulting chemical is multiplied by the expression for the holding container with respect to the number of units produced. The equations for the two chemicals added together with respect to the number of unit produced are given below:

`C_1(x)=(x)/(x+1) , C_2(x)=(2)/(x-3)`
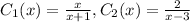
The equation for the holding container with respect to the number of unit produced is given below:

`H(x)=(x^3-9x)/(x)`

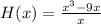
a. What rational expression do you get when you combine the two chemicals?
b. What is the simplified equation of ?
c. What would the volume be if 50, 100, or 1000 units are produced in a day?
d. The company needs a volume of 3000 How many units would need to be produced in a day?

Answer 1

`V(x) = [(x)/(x + 1) + (2)/(x-3)] * (x^3 - 9x)/(x)`

`V(x) = [((x^2-x+2)(x + 3))/((x + 1))]`

`V(50) = 2548.17`
`V(100) = 10098.10`
`V(1000) = 999201.78`

`x = 54.78`

Explanation:

Given

`V(x) = [C_1(x) + C_2(x)](H(x))`

`C_1(x) = (x)/(x+1)`

`C_1(x) = (2)/(x-3)`

`H(x) = (x^3 - 9x)/(x)`

Solving (a): Expression for V(x)

We have:

`V(x) = [C_1(x) + C_2(x)](H(x))`

Substitute known values

`V(x) = [(x)/(x + 1) + (2)/(x-3)] * (x^3 - 9x)/(x)`

Solving (b): Simplify V(x)

We have:

`V(x) = [(x)/(x + 1) + (2)/(x-3)] * (x^3 - 9x)/(x)`

Solve the expression in bracket

`V(x) = [(x*(x-3) + 2*(x+1))/((x + 1)(x -3))] * (x^3 - 9x)/(x)`

`V(x) = [(x^2-3x + 2x+2)/((x + 1)(x -3))] * (x^3 - 9x)/(x)`

`V(x) = [(x^2-x+2)/((x + 1)(x -3))] * (x^3 - 9x)/(x)`

Factor out x

`V(x) = [(x^2-x+2)/((x + 1)(x -3))] * (x(x^2 - 9))/(x)`

`V(x) = [(x^2-x+2)/((x + 1)(x -3))] * (x^2 - 9)`

Express as difference of two squares

`V(x) = [(x^2-x+2)/((x + 1)(x -3))] * (x- 3)(x + 3)`

Cancel out x - 3

`V(x) = [(x^2-x+2)/((x + 1))] *(x + 3)`

`V(x) = [((x^2-x+2)(x + 3))/((x + 1))]`

Solving (c): V(50), V(100), V(1000)

`V(x) = [((x^2-x+2)(x + 3))/((x + 1))]`

Substitute 50 for x

`V(50) = [((50^2-50+2)(50 + 3))/((50 + 1))]`

`V(50) = ((2452)(53))/((51))]`

`V(50) = 2548.17`

Substitute 100 for x

`V(100) = [((100^2-100+2)(100 + 3))/((100 + 1))]`

`V(100) = (9902)(103))/((101))`

`V(100) = 10098.10`

Substitute 1000 for x

`V(1000) = [((1000^2-1000+2)(1000 + 3))/((1000 + 1))]`

`V(1000) = [((999002)(10003))/((10001))]`

`V(1000) = 999201.78`

Solving (d): V(x) = 3000, find x

`V(x) = [((x^2-x+2)(x + 3))/((x + 1))]`

`3000 = [((x^2-x+2)(x + 3))/((x + 1))]`

Cross multiply

`3000(x + 1) = (x^2-x+2)(x + 3)`

Equate to 0

`(x^2-x+2)(x + 3)-3000(x + 1)=0`

Open brackets

`x^3 - x^2 + 2x + 3x^2 - 3x + 6 - 3000x - 3000 = 0`

Collect like terms

`x^3 + 3x^2- x^2 + 2x - 3x - 3000x + 6 - 3000 = 0`

`x^3 + x^2 -3001x -2994 = 0`

Solve using graphs (see attachment)

`x = -54.783` or

`x = -0.998` or

`x = 54.78`

x can't be negative. So:

`x = 54.78`