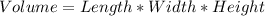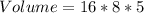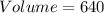Answer:
(a)
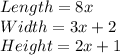
(b)
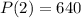
(c)
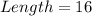
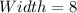
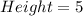
(d)
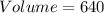
Explanation:
Given
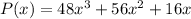
Solving (a): The prism dimension
We have:
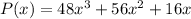
Factor out 8x
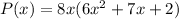
Expand 7x
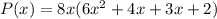
Factorize
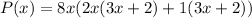
Factor out 3x + 2
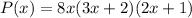
So, the dimensions are:
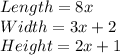
Solving (b): The volume when
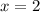
We have:
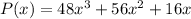
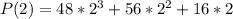
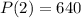
Solving (c): The dimensions when
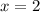
We have:
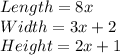
Substitute 2 for x
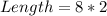
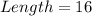
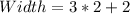
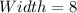

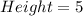
So, we have:
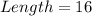
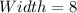
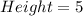
Solving (d), the volume in (c)
We have: