We need not consider a whole triangle but just point B.
Before reflection we know that
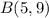 .
.
Reflecting B over
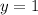 is relatively easy. First because its a reflection over the horizontal line the only coordinates that will change are y coordinates, while x coordinate will not change so half of the reflection is already done for us,
is relatively easy. First because its a reflection over the horizontal line the only coordinates that will change are y coordinates, while x coordinate will not change so half of the reflection is already done for us,
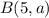
Now to what has changed, well currently the distance between 9 and 1 on the y axis is 8 up. But because we are reflecting the a must now be 8 down from 1 which means
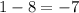 so our point is now
so our point is now
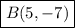 .
.
Hope this helps :)