Question

Help me solve this trig

Answer 1

Hello there!

Previously, we learnt that to solve the equation, we have to isolate the sin, cos, tan, etc first.

First Question

The first question has sin both sides. Notice that if we move sin(theta) to left. We get:-

`\displaystyle \large{2 {sin}^(2) \theta - sin \theta = 0}`

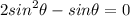
We can common factor out the expression.

`\displaystyle \large{sin \theta(2sin \theta - 1) = 0}`

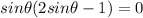
It is a trigonometric equation in quadraric pattern.

We consider both equations:-

First Equation

`\displaystyle \large{sin \theta = 0}`

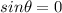
Remind that sin = y. When sin theta = 0. It means that it lies on the positive x-axis.

We know that 0 satisfies the equation, because sin(0) is 0.

Same goes for π as well, but 2π does not count because the interval is from 0 ≤ theta < 2π.

Hence:-

`\displaystyle \large { \theta = 0,\pi}`

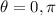
Second Equation

`\displaystyle \large{2sin \theta - 1 = 0}`

First, as we learnt. We isolate sin.

`\displaystyle \large{sin \theta = (1)/(2) }`

We know that, sin is positive in Quadrant 1 and 2.

As we learnt from previous question, we use π - (ref. angle) to find Q2 angle.

We know that sin(π/6) is 1/2. Hence π/6 is our reference angle. Since π/6 is in Q1, we only have to find Q2.

Find Quadrant 2

`\displaystyle \large{\pi - (\pi)/(6) = (6\pi)/(6) - (\pi)/(6) } \\ \displaystyle \large{ (5\pi)/(6) }`

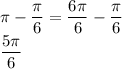
Hence:-

`\displaystyle \large{ \theta = (\pi)/(6) , (5\pi)/(6) }`

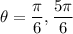
Since both first and second equations are apart of same equation. Therefore, mix both theta from first and second.

Therefore, the solutions to the first question:-

`\displaystyle \large \boxed{ \theta = 0,\pi, (\pi)/(6) , (5\pi)/(6) }`

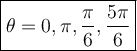
Second Question

This one is a reciprocal of tan, also known as cot.

`\displaystyle \large{cot3 \theta = 1}`

For this, I will turn cot to 1/tan.

`\displaystyle \large{ (1)/(tan3 \theta) = 1}`

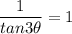
Multiply whole equation by tan3 theta, to get rid of the denominator.

`\displaystyle \large{ (1)/(tan3 \theta) * tan3 \theta = 1 * tan3 \theta } \\ \displaystyle \large{ 1= tan3 \theta }`

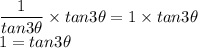
We also learnt about how to deal with number beside theta.

We increase the interval, by multiplying with the number.

Since our interval is:-

`\displaystyle \large{0 \leqslant \theta < 2\pi}`

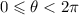
Multiply the whole interval by 3.

`\displaystyle \large{0 * 3 \leqslant \theta * 3 < 2\pi * 3} \\ \displaystyle \large{0 \leqslant 3 \theta < 6\pi }`

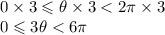
We also know that tan is positive in Quadrant 1 and Quadrant 3.

and tan(π/4) is 1. Therefore, π/4 is our reference angle and our first theta value.

When we want to find Quadrant 3, we use π + (ref. angle).

Find Q3

`\displaystyle \large{\pi + (\pi)/(4) } = (5\pi)/(4)`

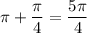
Hence, our theta values are π/4 and 5π/4. But that is for [0,2π) interval. We want to find theta values over [0,6π) interval.

As we learnt previously, that we use theta + 2πk to find values that are in interval greater than 2π.

As for tangent, we use:-

`\displaystyle \large{ \theta + \pi k = \theta}`

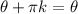
Because tan is basically a slope or line proportional graph. So it gives the same value every π period.

Now imagine a unit circle, and make sure to have some basic geometry knowledge. Know that when values addition by 180° or π would give a straight angle.

We aren't using k = 1 for this because we've already found Q3 angle.

Since we know Q1 and Q3 angle in [0,2π).

We can also use theta + 2πk if you want.

First Value or π/4

`\displaystyle \large{ (\pi)/(4) + 2\pi = (9\pi)/(4) } \\ \displaystyle \large{ (\pi)/(4) + 4\pi = (17\pi)/(4) }`

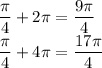
Second Value or 5π/4

`\displaystyle \large{ (5\pi)/(4) + 2\pi = (13\pi)/(4) } \\ \displaystyle \large{ (5\pi)/(4) + 4\pi = (21\pi)/(4) }`

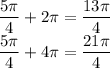
Yes, I use theta + 2πk for finding other values.

Therefore:-

`\displaystyle \large{3 \theta = (\pi)/(4) , (5\pi)/(4) , (9\pi)/(4), (17\pi)/(4) , (13\pi)/(4) , (21\pi)/(4) }`

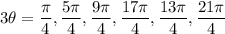
Then we divide every values by 3.

`\displaystyle \large \boxed{\theta = (\pi)/(12) , (5\pi)/(12) , (9\pi)/(12), (17\pi)/(12) , (13\pi)/(12) , (21\pi)/(12) }`

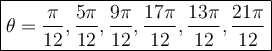
Let me know if you have any questions!