Answer:
The 19th term is 99.
Explanation:
We can write a direct formula and use it to find the 19th term. Recall that the direct formula for an arithmetic sequence is given by:
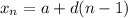
Where a is the initial term and d is the common difference.
Since the first term is 9 and the common difference is 5:

To find the 19th term, let n = 19. Thus:

And evaluate:
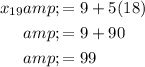
The 19th term is 99.