Question

In a survey of women in a certain country the mean height was 62.9 inches with a standard deviation of 2.81 inches answer the followinv questions about the specified normal distribution

Answer 1

The question is incomplete. The complete question is :

In a survey of women in a certain country ( ages 20-29), the mean height was 62.9 inches with a standard deviation of 2.81 inches. Answer the following questions about the specified normal distribution. (a) What height represents the 99th percentile? (b) What height represents the first quartile? (Round to two decimal places as needed)

Solution :

Let the random variable X represents the height of women in a country.

Given :

X is normal with mean, μ =
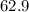`62.9` inches and the standard deviation, σ =
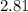`2.81` inches

Let,

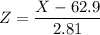`$Z=(X - 62.9)/(2.81)$` , then Z is a standard normal

a). Let the
`99th` percentile is = a

The point a is such that,

`$P(X<a)=0.99$`

`$P \left( Z < (a-62.9)/(2.81) \right) = 0.99$`

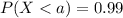
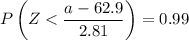
From standard table, we get :
`P( Z < 2.3263) =0.99`

∴
`$((a-62.9))/(281) = 2.3263$`

`$a= (2.3263 * 2.81 ) +62.9$`

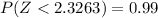
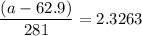
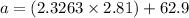
= 6.536903 + 62.9

= 69.436903

= 69.5 (rounding off)

Therefore, the height represents the
`99th` percentile = 69.5 inches.

b). Let b = height represents the first quartile.

It is given by :

`P( X < b) =0.25`

`$P \left( Z < ((b-62.9))/(2.81) \right) = 0.25$`

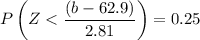
From the standard normal table,

`P( Z < -0.6745) =0.99`

∴
`$((b-62.9))/(2.81)= 0.6745$`

`$b=(0.6745 * 2.81) +62.9$`

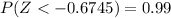
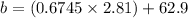
= 1.895345 + 62.9

= 64.795345

= 64.8 (rounding off)

Therefore, the height represents the 1st quartile is 64.8 inches.