Question

4.

A line contains the points R (-5, -6) S (1, 5) and T (x, 10). Solve for x. Be sure to show and explain all work

Answer 1

x is 3.
`\overline{72}`

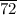
Explanation:

The given points on the line are;

R(-5, -6), S(1, 5) and T(x, 10)

The number of points required to find the equation of the line = 2 points

The slope, m, of the line using points R(-5, -6) and S(1, 5) is given as follows;

m = (5 - (-6))/(1 - (-5)) = 11/6

The equation of the line in slope and point form, using point S(1, 5) is therefore;

y - 5 = (11/6)·(x - 1) = 11·x/6 - 11/6

y - 5 = 11·x/6 - 11/6, given that the x-value is required, we have;

x = (y - 5 + 11/6) × 6/11 = 6·y/11 - 19/11

x = 6·y/11 - 19/11

At point T(x, 10), y = 10, therefore, we have;

x = 6×10/11 - 19/11 = 41/11 = 3.
`\overline{72}`

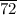
x = 3.
`\overline{72}`.