Question

(a) The radius of a circle is 5.6 cm. Find the angle in degrees subtended by an arc of 22 cm at the

centre of the circle.



DO NO A PLEASE​

Answer 1

225 degrees

Explanation:

Given the following data;

• Radius, r = 5.6 cm
• Length of arc = 22 cm

To find the angle in degrees subtended by an arc;

Mathematically, the length of the arc of a circle is given by the formula;

S = rA

Where;

• S is the length of the arc.
• A is the angle measured in radians.

Substituting the values into the formula, we have;

22 = 5.6 * A

`A = \frac {22}{5.6}`

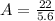
A = 3.9286 radians.

Next, we would convert the value of the angle in radians to degrees;

Conversion:

`1 \; radian = \frac {180}{\pi} \; degrees`

`3.9286 \; radians = X \; degrees`

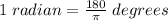
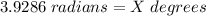
Cross-multiplying, we have;

`X = \frac {180}{\frac {22}{7}} * 3.9286`

`X = \frac {180 * 7}{22} * 3.9286`

`X = \frac {1260}{22} * 3.9286`

`X = 57.2727 * 3.9286`

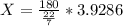
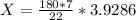
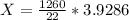
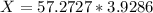
X = 225.0015 ≈ 225 degrees