9514 1404 393
Answer:
5. x = (6 +√7)/29; a=6, b=1, c=29
6. x = 2
Explanation:
5.
The quadratic formula can be used, where a=(5+4√7), b=(4-2√7), c=-1.
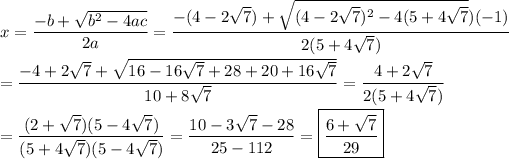
__
6.
Use the substitution z=3^x to put the equation in the form ...
z² -3z -54 = 0
(z -9)(z +6) = 0 . . . . . factor
z = 9 or -6 . . . . . . . . value of z that make the factors zero
Only the positive solution is useful, since 3^x cannot be negative.
z = 9 = 3^2 = 3^x . . . . use the value of z to find x
x = 2