Question

How to solve this trig

Answer 1

Hi there!

To find the Trigonometric Equation, we have to isolate sin, cos, tan, etc. We are also given the interval [0,2π).

First Question

What we have to do is to isolate cos first.

`\displaystyle \large{ cos \theta = - (1)/(2) }`

Then find the reference angle. As we know cos(π/3) equals 1/2. Therefore π/3 is our reference angle.

Since we know that cos is negative in Q2 and Q3. We will be using π + (ref. angle) for Q3. and π - (ref. angle) for Q2.

Find Q2

`\displaystyle \large{ \pi - ( \pi)/(3) = (3 \pi)/(3) - ( \pi)/(3) } \\ \displaystyle \large \boxed{ (2 \pi)/(3) }`

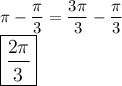
Find Q3

`\displaystyle \large{ \pi + ( \pi)/(3) = (3 \pi)/(3) + ( \pi)/(3) } \\ \displaystyle \large \boxed{ (4 \pi)/(3) }`

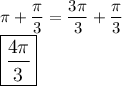
Both values are apart of the interval. Hence,

`\displaystyle \large \boxed{ \theta = (2 \pi)/(3) , (4 \pi)/(3) }`

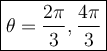
Second Question

Isolate sin(4 theta).

`\displaystyle \large{sin 4 \theta = - (1)/( √(2) ) }`

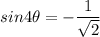
Rationalize the denominator.

`\displaystyle \large{sin4 \theta = - ( √(2) )/(2) }`

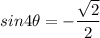
The problem here is 4 beside theta. What we are going to do is to expand the interval.

`\displaystyle \large{0 \leqslant \theta < 2 \pi}`

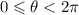
Multiply whole by 4.

`\displaystyle \large{0 * 4 \leqslant \theta * 4 < 2 \pi * 4} \\ \displaystyle \large \boxed{0 \leqslant 4 \theta < 8 \pi}`

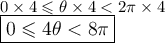
Then find the reference angle.

We know that sin(π/4) = √2/2. Hence π/4 is our reference angle.

sin is negative in Q3 and Q4. We use π + (ref. angle) for Q3 and 2π - (ref. angle for Q4.)

Find Q3

`\displaystyle \large{ \pi + ( \pi)/(4) = ( 4 \pi)/(4) + ( \pi)/(4) } \\ \displaystyle \large \boxed{ (5 \pi)/(4) }`

Find Q4

`\displaystyle \large{2 \pi - ( \pi)/(4) = (8 \pi)/(4) - ( \pi)/(4) } \\ \displaystyle \large \boxed{ (7 \pi)/(4) }`

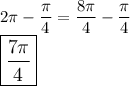
Both values are in [0,2π). However, we exceed our interval to < 8π.

We will be using these following:-

`\displaystyle \large{ \theta + 2 \pi k = \theta \: \: \: \: \: \sf{(k \: \: is \: \: integer)}}`

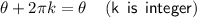
Hence:-

For Q3

`\displaystyle \large{ (5 \pi)/(4) + 2 \pi = (13 \pi)/(4) } \\ \displaystyle \large{ (5 \pi)/(4) + 4\pi = (21 \pi)/(4) } \\ \displaystyle \large{ (5 \pi)/(4) + 6\pi = (29 \pi)/(4) }`

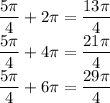
We cannot use any further k-values (or k cannot be 4 or higher) because it'd be +8π and not in the interval.

For Q4

`\displaystyle \large{ ( 7 \pi)/(4) + 2 \pi = (15 \pi)/(4) } \\ \displaystyle \large{ ( 7 \pi)/(4) + 4 \pi = (23\pi)/(4) } \\ \displaystyle \large{ ( 7 \pi)/(4) + 6 \pi = (31 \pi)/(4) }`

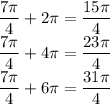
Therefore:-

`\displaystyle \large{4 \theta = (5 \pi)/(4) , (7 \pi)/(4) , (13\pi)/(4) , (21\pi)/(4) , (29\pi)/(4), (15 \pi)/(4) , (23\pi)/(4) , (31\pi)/(4) }`

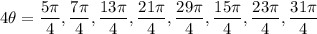
Then we divide all these values by 4.

`\displaystyle \large \boxed{\theta = (5 \pi)/(16) , (7 \pi)/(16) , (13\pi)/(16) , (21\pi)/(16) , (29\pi)/(16), (15 \pi)/(16) , (23\pi)/(16) , (31\pi)/(16) }`

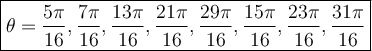
Let me know if you have any questions!