Answer:
C. 540 N
Step-by-step explanation:
Let suppose that system formed by the athlete and the load are in equilibrium. By Newton's Laws of Motion, we use the moment equation with respect to the feet of the athlete to determine the upward force exerted by his two arms:
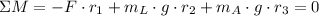
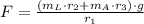 (1)
(1)
Where:
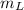 - Mass of the load, in kilograms.
- Mass of the load, in kilograms.
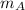 - Mass of the athlete, in kilograms.
- Mass of the athlete, in kilograms.
 - Gravitational acceleration, in meters per square second.
- Gravitational acceleration, in meters per square second.
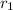 ,
,
 ,
,
 - Distances with respect to the feet, in meters.
- Distances with respect to the feet, in meters.
 - Upward force exerted by his two arms, in newtons.
- Upward force exerted by his two arms, in newtons.
If
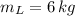 ,
,
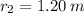 ,
,
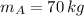 ,
,
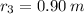 ,
,
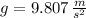 and
and
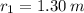 , then the upward force is:
, then the upward force is:
![F = ([(6\,kg)\cdot (1.20\,m)+(70\,kg)\cdot (0.90\,m)]\cdot \left(9.807\,(m)/(s^(2)) \right))/(1.30\,m)](https://img.qammunity.org/2022/formulas/physics/high-school/qphkl3fabjdma1s9lpvsqhy37j2sbftjby.png)
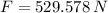
The upward force exerted by his two arms is 529.578 newtons. (Right answer: C)