Answer:
The width is:

And the length is:
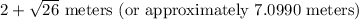
Explanation:
Recall that the area of a rectangle is given by:
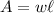
Where w is the width and l is the length.
We are given that the length of a rectangle is four meters longer than the width. Thus:
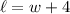
And we also know that the area of the rectangle is 22 square meteres.
Substitute:
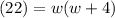
Distribute and isolate the equation:
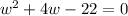
The equation isn't factorable, so we can instead use the quadratic formula:
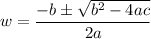
In this case, a = 1, b = 4, and c = -22. Substitute:
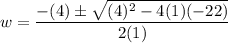
Evaluate:
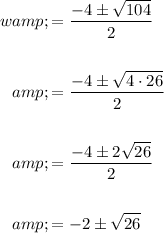
Thus, our two solutions are:
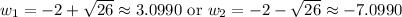
Since the width cannot be negative, we can ignore the second solution.
Since the length is four meters longer than the width:
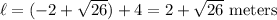
Thus, the dimensions of the rectangle are:
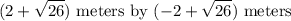
Or, approximately 3.0990 by 7.0990.