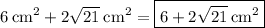Answer:
Explanation:
The quadrilateral ABCD consists of two triangles. By adding the area of the two triangles, we get the area of the entire quadrilateral.
Vertices A, B, and C form a right triangle with legs
 ,
,
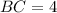 , and
, and
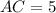 . The two legs, 3 and 4, represent the triangle's height and base, respectively.
. The two legs, 3 and 4, represent the triangle's height and base, respectively.
The area of a triangle with base
 and height
and height
 is given by
is given by
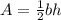 . Therefore, the area of this right triangle is:
. Therefore, the area of this right triangle is:
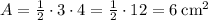
The other triangle is a bit trickier. Triangle
 is an isosceles triangles with sides 5, 5, and 4. To find its area, we can use Heron's Formula, given by:
is an isosceles triangles with sides 5, 5, and 4. To find its area, we can use Heron's Formula, given by:
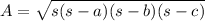 , where
, where
 ,
,
 , and
, and
 are three sides of the triangle and
are three sides of the triangle and
 is the semi-perimeter (
is the semi-perimeter (
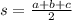 ).
).
The semi-perimeter,
 , is:
, is:
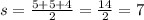
Therefore, the area of the isosceles triangle is:
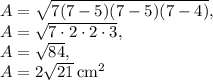
Thus, the area of the quadrilateral is: