Question

`\lim_(x\to \ 0) \frac{√(cos2x)-\sqrt[3]{cos3x} }{sinx^(2) }`

Answer 1

`\displaystyle \lim_(x \to 0) \frac{√(cos(2x)) - \sqrt[3]{cos(3x)}}{sin(x^2)} = (1)/(2)`

General Formulas and Concepts:

Calculus

Limits

Limit Rule [Variable Direct Substitution]:
`\displaystyle \lim_(x \to c) x = c`

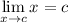
L'Hopital's Rule

Differentiation

• Derivatives
• Derivative Notation

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Explanation:

We are given the limit:

`\displaystyle \lim_(x \to 0) \frac{√(cos(2x)) - \sqrt[3]{cos(3x)}}{sin(x^2)}`

When we directly plug in x = 0, we see that we would have an indeterminate form:

`\displaystyle \lim_(x \to 0) \frac{√(cos(2x)) - \sqrt[3]{cos(3x)}}{sin(x^2)} = (0)/(0)`

This tells us we need to use L'Hoptial's Rule. Let's differentiate the limit:

`\displaystyle \lim_(x \to 0) \frac{√(cos(2x)) - \sqrt[3]{cos(3x)}}{sin(x^2)} = \displaystyle \lim_(x \to 0) \frac{(-sin(2x))/(√(cos(2x))) + \frac{sin(3x)}{[cos(3x)]^{(2)/(3)}}}{2xcos(x^2)}`

Plugging in x = 0 again, we would get:

`\displaystyle \lim_(x \to 0) \frac{(-sin(2x))/(√(cos(2x))) + \frac{sin(3x)}{[cos(3x)]^{(2)/(3)}}}{2xcos(x^2)} = (0)/(0)`

Since we reached another indeterminate form, let's apply L'Hoptial's Rule again:

`\displaystyle \lim_(x \to 0) \frac{(-sin(2x))/(√(cos(2x))) + \frac{sin(3x)}{[cos(3x)]^{(2)/(3)}}}{2xcos(x^2)} = \lim_(x \to 0) \frac{\frac{-[cos^2(2x) + 1]}{[cos(2x)]^{(2)/(3)}} + \frac{cos^2(3x) + 2}{[cos(3x)]^{(5)/(3)}}}{2cos(x^2) - 4x^2sin(x^2)}`

Substitute in x = 0 once more:

`\displaystyle \lim_(x \to 0) \frac{\frac{-[cos^2(2x) + 1]}{[cos(2x)]^{(2)/(3)}} + \frac{cos^2(3x) + 2}{[cos(3x)]^{(5)/(3)}}}{2cos(x^2) - 4x^2sin(x^2)} = (1)/(2)`

And we have our final answer.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits