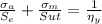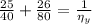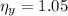Question

A bar of steel has the minimum properties Se = 40 kpsi, Sy = 60 kpsi, and Sut = 80 ksi. The bar is subjected to a steady torsional stress of 15 kpsi and an alternating bending stress of 25 ksi. Find the factor of safety guarding against a static failure, and either the factor of safety guarding against a fatigue failure or the expected life of the part. For the fatigue analysis use Modified Goodman criterion.

Answer 1

The correct solution is:

(a) 1.66

(b) 1.05

Step-by-step explanation:

Given:

Bending stress,

`\sigma_b = 25 \ kpsi`

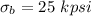
Torsional stress,

`\tau= 15 \ kpsi`

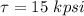
Yield stress of steel bar,

`\delta_y = 60 \ kpsi`

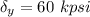
As we know,

⇒
`\sigma_(max)^' \ = √(\sigma_b^2 + 3 \gamma^2)`

`= √((25)^2+3(15)^2)`

`=36.055 \ kpsi`

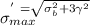
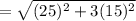
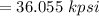
(a)

The factor of safety against static failure will be:

⇒
`\eta_y = (\delta_y)/(\sigma_(max)^')`

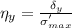
By putting the values, we get

`=(60)/(36.055)`

`=1.66`

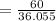
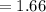
(b)

According to the Goodman line failure,

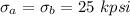
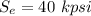
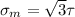
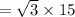
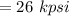
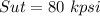
`\sigma_a = \sigma_b = 25 \ kpsi`

`S_e = 40 \ kpsi`

`\sigma_m = √(3) \tau`

`=√(3)* 15`

`=26 \ kpsi`

`Sut = 80 \ kpsi`

⇒
`(\sigma_a)/(S_e) +(\sigma_m)/(Sut) =(1)/(\eta_y)`

`(25)/(40)+(26)/(80)=(1)/(\eta_y)`

`\eta_y = 1.05`