Given:
Amplitude = 21
Vertical shift = 19 units down
To find:
The maximum and the minimum value.
Solution:
The general form of sine function is:

Where, |A| is amplitude,
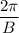 is period,
is period,
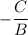 is phase shift and D is the vertical shift.
is phase shift and D is the vertical shift.
Here,
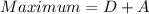

We have,
Amplitude:
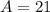
Vertical shift:
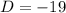
Negative sign means shifts downwards.
Now,
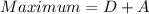
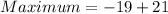
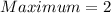
And,

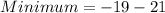
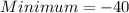
Therefore, the minimum value is -40 and the maximum value is 2.