Question

If a sine curve has a vertical shift down 19 units with an amplitude of 21, what will the minimum and maximum values be? (i.e. how high and low will the graph go?)

Min Value:
Max Value:

Answer 1

Given:

Amplitude = 21

Vertical shift = 19 units down

To find:

The maximum and the minimum value.

Solution:

The general form of sine function is:

`y=A\sin (Bx+C)+D`

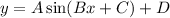
Where, |A| is amplitude,
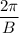`(2\pi)/(B)` is period,
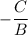`-(C)/(B)` is phase shift and D is the vertical shift.

Here,

`Maximum=D+A`

`Minimum=D-A`

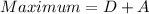
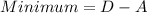
We have,

Amplitude:
`A = 21`

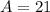
Vertical shift:
`D=-19`

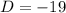
Negative sign means shifts downwards.

Now,

`Maximum=D+A`

`Maximum=-19+21`

`Maximum=2`

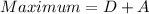
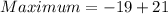
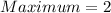
And,

`Minimum=D-A`

`Minimum=-19-21`

`Minimum=-40`

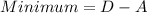
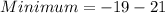
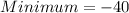
Therefore, the minimum value is -40 and the maximum value is 2.