Question

When a sprinkler is installed in the ground, the spray of water goes up and falls in the pattern of a parabola. The height, in inches, of a spray of water is given by the equation h(x)=160x−16x2 where x is the number of feet away from the sprinkler head the spray is. What is the height of the spray 2 feet away from the sprinkler head?

Answer 1

(1) 256 inches

(2) 5 feet

(3) 400 inches

(4) 10 feet

Explanation:

(1) The function that gives the height in inches of the spray of water at a distance x from the sprinkler head is given as follows;

h(x) = 160·x - 16·x²

At x = 2 feet, we have;

h(2) = 160 × 2 - 16 × 2² = 256

Therefore, the height of the spray water at a horizontal distance of 2 feet from the sprinkler head h(2) = 256 inches

(2) The x-coordinate,
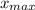`x_(max)`, of the maximum point of a parabola given in the form, y = a·x² + b·x + c is found using the following formula;

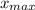`x_(max)` = -b/(2·a)

The x-coordinate,
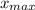`x_(max)`, of the maximum point of the given equation of the parabola, h(x) = 160·x - 16·x², (a = -16, b = 160) is therefore;

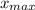`x_(max)` = -160/(2 × (-16)) = 5

Therefore, the number of feet along the way, the function will reach maximum height,
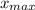`x_(max)` = 5 feet

(3) The function, h(x) = 160·x - 16·x², will reach maximum height,
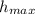`h_(max)`, at x = 5, therefore;

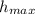`h_(max)` = h(5) = 160 × 5 - 16 × 5² = 400

The maximum height of the spray,
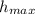`h_(max)` = 400 inches

(4) The water is at ground level where h(x) = 0, therefore;

At ground level, h(x) = 0 = 160·x - 16·x²

160·x - 16·x² = 0

∴ 16·x × (10 - x) = 0

By zero product rule, we 16·x = 0, or (10 - x) = 0, from which we have;

x = 0, or x = 10

The water is at ground level at x = 0 and x = 10 feet, therefore, the water will hit the ground again (the second time after leaving the sprinkler head at x = 0) at x = 10 feet.