Answer:
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx = -93](https://img.qammunity.org/2022/formulas/mathematics/high-school/6wysi4shwiqbvmgbl0cocg8oiy1makkrjt.png)
General Formulas and Concepts:
Calculus
Integration
Integration Property [Multiplied Constant]:
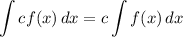
Integration Property [Addition/Subtraction]:
![\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/r5yh324r81plt97j3zrr5qi2xxczxlqi34.png)
Explanation:
Step 1: Define
Identify
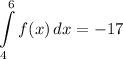
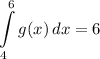
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/xy2rqqk8v5w0a4hwfzznuz1nfrmlq801zl.png)
Step 2: Integrate
- [Integral] Rewrite [Integration Property - Addition/Subtraction]:
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx = \int\limits^6_4 {3f(x)} \, dx - \int\limits^6_4 {7g(x)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/1r6mbntk3kpdlpclkp0z5h853hq8xhati5.png)
- [Integrals] Rewrite [Integration Property - Multiplied Constant]:
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx = 3 \int\limits^6_4 {f(x)} \, dx - 7 \int\limits^6_4 {g(x)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/1qkrjpziwqkh2igc2253whqe4ip0oce9yq.png)
- [Integrals] Substitute:
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx = 3(-17) - 7(6)](https://img.qammunity.org/2022/formulas/mathematics/high-school/qt3po7owfeooqo2fjrsxkuo9fa0sbelwws.png)
- Simplify:
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx = -93](https://img.qammunity.org/2022/formulas/mathematics/high-school/6wysi4shwiqbvmgbl0cocg8oiy1makkrjt.png)
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Integration