Answer:
Greatest height = 2040m (to 3 significant figures)
Horizontal displacement to the point of greatest height = 7060m (to 3 significant figures)
Step-by-step explanation:
First, we want to find the greatest height reached;
In other words, we are asked to find the maximum vertical displacement;
What should be known is that vertical quantities are, for all intents and purposes really, independent and thus unaffected by horizontal factors at play;
We can therefore calculate and proceed considering the two perpendicular planes separately;
So, we now need to consider what we know, what we need to find and what we can deduce:
We know, as given, the initial velocity and we need to find the displacement, this should indicate that we need to use the SUVAT or kinematic equations/formulas;
We can deduce that the vertical velocity at the maximum height will be 0 because at the greatest height, the projectile will no longer ascend, it will stop and then begin to fall;
And since there is a change in velocity, there is acceleration involved as well;
We are not told of any capacity of the projectile itself to accelerate so we can assume there is no acceleration from it and this leaves only gravity to consider in the vertical dimension as acceleration:
So, to summarise nicely all of the information:
u = initial velocity (m/s) = 400
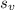 = vertical displacement or the height reached (m)
= vertical displacement or the height reached (m)
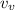 = final vertical velocity (m/s) = 0
= final vertical velocity (m/s) = 0
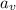 = vertical acceleration (m/s²) = -9.81 (i.e. gravity)
= vertical acceleration (m/s²) = -9.81 (i.e. gravity)
The relevant SUVAT or kinematic equation, which involves all of these quantities:
v² = u² + 2as
The only other thing we need to do before we can use this equation to get
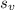 is to get the initial vertical velocity (i.e.
is to get the initial vertical velocity (i.e.
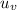 );
);
We have the initial velocity and what we can do is split the velocity into it's vertical and horizontal component;
P.S. this is a key concept in any kind of mechanics and physics questions and can be done forces, velocities or even acceleration (really cool XD)
The projection can be illustrated as a right-angle triangle with an angle of 30° and a hypotenuse of 400;
If we want to find the vertical velocity, which is what we want, we need to use trigonometry:
sin(Θ) = opposite/hypotenuse
Substitute in our values and rearrange:
sin (30) =
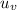 /400
/400
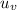 = 400.sin(30)
= 400.sin(30)
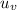 = 200
= 200
Now we can plug all these values in the aforementioned SUVAT equation:
(0)² = (200)² + 2(-9.81)(
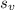 )
)
0 = 40000 - 19.62(
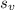 )
)
19.62(
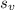 ) = 40000
) = 40000
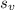 = ⁴⁰⁰⁰⁰/₁₉.₆₂
= ⁴⁰⁰⁰⁰/₁₉.₆₂
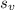 = 2038.7359836901121304791029561672 → 2040 m
= 2038.7359836901121304791029561672 → 2040 m
Now, to find how far the horizontal distance is to this point of the greatest height, we need to do something similar except we need to consider the horizontal dimension, not the vertical;
So, once again, we have initial velocity (and we can find the initial horizontal velocity) and we want to find the horizontal displacement;
In terms of acceleration, gravity is negligible since it is a vertical acceleration so it has no effect on the horizontal speed, and by extension no effect on the horizontal displacement;
Air resistance is typically ignored until higher levels of education so we can simply ignore it as well;
This means horizontal acceleration is 0;
So, to summarise:
u = initial velocity (m/s) = 400
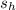 = horizontal displacement (m)
= horizontal displacement (m)
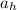 = horizontal acceleration (m/s²) = 0
= horizontal acceleration (m/s²) = 0
Since acceleration is 0, there is no change to velocity so there is no initial and final velocity;
This means the relevant equation or formula is (very easy):
v = s/t or commonly known as speed = distance/time
We want to find the distance and we have speed, we just need time;
We can find time because this variable will be the same for initial and horizontal velocities, i.e. the time taken for the projectile to reach the maximum height will be the same as the time taken to reach the point of horizontal displacement we want to find;
So to find the time taken for the vertical displacement, we can use the SUVAT formula:
s = ¹/₂(u + v).t
Plug in the values:
2038.735.... = ¹/₂(200 + 0).t
2038.735.... = 100t
t = 20.38735...
Horizontal velocity will be:
cos(Θ) = adjacent/hypotenuse
cos(30) =
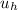 /400
/400
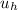 = 400.cos(30)
= 400.cos(30)
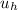 = 346.41016...
= 346.41016...
Now, we have horizontal velocity and time, we can find the horizontal displacement:
346.41... =
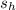 /20.387...
/20.387...
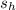 = 346.41...(20.387...)
= 346.41...(20.387...)
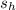 = 7062.38886.... → 7060 m
= 7062.38886.... → 7060 m
Its a bit long but is not complicated once you get it
Hope this helps ;D