First integrate the indefinite integral,
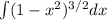
Let
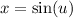 which will make
which will make
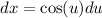 .
.
Then
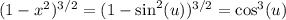 which makes
which makes
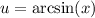 and our integral is reshaped,
and our integral is reshaped,
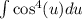
Use reduction formula,
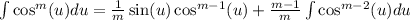
to get,
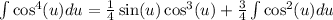
Notice that,
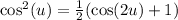
Then integrate the obtained sum,
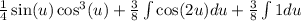
Now introduce
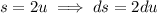 and substitute and integrate to get,
and substitute and integrate to get,
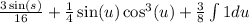
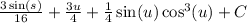
Substitute 2u back for s,
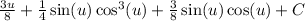
Substitute
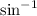 for u and simplify with
for u and simplify with
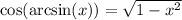 to get the result,
to get the result,
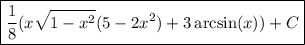
Let
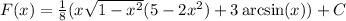
Apply definite integral evaluation from b to a,
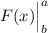 ,
,
![F(x)\Big|_b^a=F(a)-F(b)=\boxed{(1)/(8)(a√(1-a^2)(5-2a^2)+3\arcsin(a))-(1)/(8)(b√(1-b^2)(5-2b^2)+3\arcsin(b))}]()
Hope this helps :)