Question

For a given function ƒ(x) = x2 – x + 1, the operation –ƒ(x) = –(x2 – x + 1) will result in a

A) reflection across the x-axis.

B) horizontal shrink.

C) reflection across the y-axis.

D) vertical shrink.

Answer 1

A) reflection across the x-axis.

Step-by-step explanation: I took the test

Answer 2

Given:

The function is:

`f(x)=x^2-x+1`

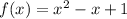
To find:

The result of the operation
`-f(x)=-(x^2-x+1)`.

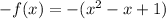Solution:

If
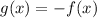`g(x)=-f(x)`, then the graph of f(x) is reflected across the x-axis to get the graph of g(x).

We have,

`f(x)=x^2-x+1`

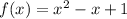
The given operation is:

`-f(x)=-(x^2-x+1)`

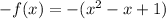
So, it will result in a reflection across the x-axis.

Therefore, the correct option is A.