Question

A 250g object hangs from a spring that has a spring constant of 48.0 N/m and oscillates with an amplitude of 5.42cm

1)The magnitude of the objects acceleration when the displacement is 4.27 cm (down) is __ m/s^2

2)Given that the object has an amplitude of 5.42 cm the maximum speed that the object is __m/s

Answer 1

Step-by-step explanation:

Given that,

Mass of an object, m = 250 g = 0.25 kg

Spring constant, k = 48 N/m

The amplitude of the oscillation, A = 5.42 cm = 0.0542 m

1. At equilibrium,

ma = kx

Where

a is the acceleration of the object

So,

`a=(kx)/(m)\\\\a=(48* 0.0542)/(0.25)\\\\a=10.4\ m/s^2`

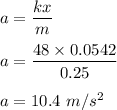
2. The maximum speed of the object is :

`v=A\omega\\\\v=A\sqrt{(k)/(m)}\\\\v=0.0542* \sqrt{(48)/(0.25)}\\\\v=0.75\ m/s`

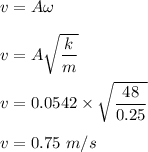
Hence, this is the required solution.