Question

Help with q25 please. Thanks.​

Answer 1

First, I'll make f(x) = sin(px) + cos(px) because this expression shows up quite a lot, and such a substitution makes life a bit easier for us.

Let's apply the first derivative of this f(x) function.

`f(x) = \sin(px)+\cos(px)\\\\f'(x) = (d)/(dx)[f(x)]\\\\f'(x) = (d)/(dx)[\sin(px)+\cos(px)]\\\\f'(x) = (d)/(dx)[\sin(px)]+(d)/(dx)[\cos(px)]\\\\f'(x) = p\cos(px)-p\sin(px)\\\\ f'(x) = p(\cos(px)-\sin(px))\\\\`

Now apply the derivative to that to get the second derivative

`f''(x) = (d)/(dx)[f'(x)]\\\\f''(x) = (d)/(dx)[p(\cos(px)-\sin(px))]\\\\ f''(x) = p*\left((d)/(dx)[\cos(px)]-(d)/(dx)[\sin(px)]\right)\\\\ f''(x) = p*\left(-p\sin(px)-p\cos(px)\right)\\\\ f''(x) = -p^2*\left(\sin(px)+\cos(px)\right)\\\\ f''(x) = -p^2*f(x)\\\\`

We can see that f '' (x) is just a scalar multiple of f(x). That multiple of course being -p^2.

Keep in mind that we haven't actually found dy/dx yet, or its second derivative counterpart either.

-----------------------------------

Let's compute dy/dx. We'll use f(x) as defined earlier.

`y = \ln\left(\sin(px)+\cos(px)\right)\\\\y = \ln\left(f(x)\right)\\\\(dy)/(dx) = (d)/(dx)\left[y\right]\\\\(dy)/(dx) = (d)/(dx)\left[\ln\left(f(x)\right)\right]\\\\(dy)/(dx) = (1)/(f(x))*(d)/(dx)\left[f(x)\right]\\\\(dy)/(dx) = (f'(x))/(f(x))\\\\`

Use the chain rule here.

There's no need to plug in the expressions f(x) or f ' (x) as you'll see in the last section below.

Now use the quotient rule to find the second derivative of y

`(d^2y)/(dx^2) = (d)/(dx)\left[(dy)/(dx)\right]\\\\(d^2y)/(dx^2) = (d)/(dx)\left[(f'(x))/(f(x))\right]\\\\(d^2y)/(dx^2) = (f''(x)*f(x)-f'(x)*f'(x))/((f(x))^2)\\\\(d^2y)/(dx^2) = (f''(x)*f(x)-(f'(x))^2)/((f(x))^2)\\\\`

If you need a refresher on the quotient rule, then

`(d)/(dx)\left[(P)/(Q)\right] = (P'*Q - P*Q')/(Q^2)\\\\`

where P and Q are functions of x.

-----------------------------------

This then means

`(d^2y)/(dx^2) + \left((dy)/(dx)\right)^2 + p^2\\\\(f''(x)*f(x)-(f'(x))^2)/((f(x))^2) + \left((f'(x))/(f(x))\right)^2 + p^2\\\\(f''(x)*f(x)-(f'(x))^2)/((f(x))^2) +((f'(x))^2)/((f(x))^2) + p^2\\\\(f''(x)*f(x)-(f'(x))^2+(f'(x))^2)/((f(x))^2) + p^2\\\\(f''(x)*f(x))/((f(x))^2) + p^2\\\\`

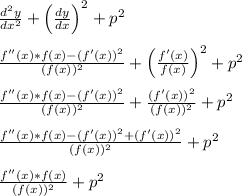
Note the cancellation of -(f ' (x))^2 with (f ' (x))^2

------------------------------------

Let's then replace f '' (x) with -p^2*f(x)

This allows us to form ( f(x) )^2 in the numerator to cancel out with the denominator.

`(f''(x)*f(x))/((f(x))^2) + p^2\\\\(-p^2*f(x)*f(x))/((f(x))^2) + p^2\\\\(-p^2*(f(x))^2)/((f(x))^2) + p^2\\\\-p^2 + p^2\\\\0\\\\`

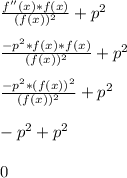
So this concludes the proof that
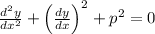`(d^2y)/(dx^2) + \left((dy)/(dx)\right)^2 + p^2 = 0\\\\` when
`y = \ln\left(\sin(px)+\cos(px)\right)\\\\`

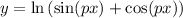
Side note: This is an example of showing that the given y function is a solution to the given second order linear differential equation.