Answer:
y=4x-3
Explanation:
Hi there!
We are given the points (1,1) and (-2, -11) and we want to write the equation of the line in slop-intercept form
Slope-intercept form is given as y=mx+b, where m is the slope and b is the y intercept
So let's find the slope of the line
The formula for the slope calculated from two points is
 , where
, where
 and
and
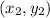 are points
are points
We have everything we need to calculate the slope, let's just label the points to avoid confusion
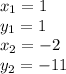
Now substitute those values into the formula
m=

m=
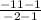
Subtract
m=
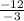
Divide
m=4
So the slope of the line is 4
Here is the equation of the line so far:
y=4x+b
We need to find b
As the equation passes through both (1,1) and (-2, -11), we can plug either one of them into the equation to solve for b
Taking (1,1) will give us this:
1=4(1)+b
Multiply
1=4+b
Subtract 4 from both sides
-3=b
Substitute -3 as b into the equation
y=4x-3
Hope this helps!