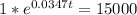Answer:
0.0347 = constant of proportionality
Explanation:
Given
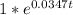
Solving (a): what does 0.0347 represent?
An exponential model is represented as:
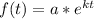
Where:
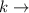 constant of proportionality
constant of proportionality
So, by comparison:
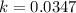
Hence:
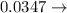 constant of proportionality
constant of proportionality
Solving (b): Formula to calculate when balance equals 15000
To do this, we simply equate the formula to 15000.
So, we have: