Answer:

Step-by-step explanation:
We are asked to find the pressure on a gas given a change in volume. We will use Boyle's Law which states the volume of a gas is inversely proportional to the pressure. The formula for this law is:
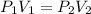
The gas originally has a pressure of 9.5 atmospheres and a volume of 1.7 liters.
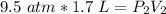
The gas is compressed to a volume of 1.1 liters, but the pressure is unknown.
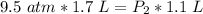
We want to find the new pressure, so we must isolate the variable P₂. It is being multiplied by 1.1 liters. The inverse operation of multiplication is division. Divide both sides of the equation by 1.1 L.
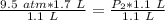
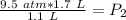
The units of liters cancel.
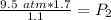
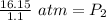

Round to the tenths place. The 8 in the hundredth place tells us to round the 6 up to a 7.

The new pressure at a volume of 1.1 liters is approximately 14.7 atmospheres.