Given:
The function is:
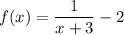
To find:
The graph of the given function.
Solution:
We have,
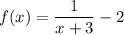
It can be written as:
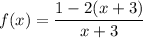
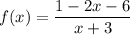
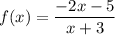
Putting
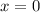 to find the y-intercept.
to find the y-intercept.

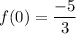
So, the y-intercept is
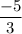 .
.
Putting
 to find the x-intercept.
to find the x-intercept.
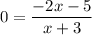
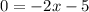
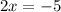
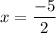

So, the x-intercept is
 .
.
For vertical asymptote, equate the denominator and 0.
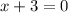

So, the vertical asymptote is
 .
.
The degrees of numerator and denominator are equal, so the horizontal asymptote is the ratio of leading coefficients.
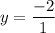
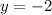
So, the horizontal asymptote is
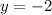 .
.
End behavior of the given function:
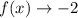 as
as
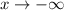
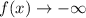 as
as
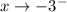
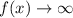 as
as
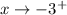
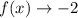 as
as
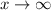
Using all these key features, draw the graph of given function as shown below.