Question

Which function best fits the following points?

A. y= -12.84032 + 0.0225x
B. y = 65.0778 × 772.9605^x
C. y = -197.0571x^2 + 245.6243x + 6.0321
D. None of the above​

Answer 1

Given:

The graph of a scatter plot.

To find:

The function that best fits the given points.

Solution:

From the given graph it is clear that the linear function is the best fit for the given points because the points lie on a straight line or near to it.

So, options B and C are incorrect because they represent exponential and quadratic function respectively.

Let as assume the two points on the graph are (0.80,-12.82) and (2,-12.79).

Using this two points, the equation of line is:

`y-(-12.82)=(-12.79-(-12.82))/(2-0.80)(x-0.80)`

`y+12.82=(-12.79+12.82)/(2-0.80)(x-0.80)`

`y+12.82=0.025(x-0.80)`

`y+12.82=0.025x-0.02`

`y=0.025x-0.02-12.82`

`y=0.025x-12.84`

`y=-12.84+0.025x`

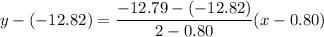
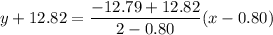
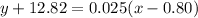
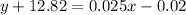
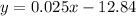
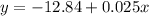
It is the approximate function to the function that is in option A.

Therefore, the correct option is A.