I assume you're supposed to find the limit as n approaches infinity, not x.
You have
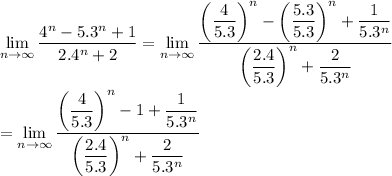
For |x| < 1, we have lim |x|ⁿ = 0 as n goes to infinity. Then each exponential term converges to 0, which leaves us with -1/0. This means the limit is negative infinity.
On the other hand, perhaps you meant to write
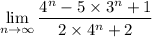
The same algebraic manipulation gives us
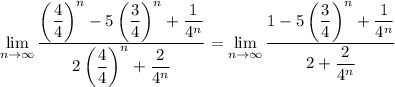
Again the exponential terms converge to 0, but this time we're left with the limit 1/2.