Question

Which of the following represents the factorization of the trinomial below?

- 4x3 - 4x2 +24 x
O A. -4(x2-2)(x+3)
B. -4(x2 + 2)(x+3)
O C. -4x(x + 2)(x+3)
D. -4x(x - 2)(x+3)

Answer 1

D. -4x(x - 2)(x+3)

Explanation:

We are given the following trinomial:

`-4x^3 - 4x^2 + 24x`

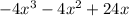
-4x is the common term, so:

`-4x((-4x^3)/(-4x) - (4x^2)/(-4x^3) + (24x)/(-4x)) = -4x(x^2+x-6)`

The second degree polynomial can also be factored, finding it's roots.

Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

This polynomial has roots
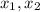`x_(1), x_(2)` such that
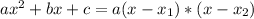`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\Delta))/(2*a)`

`x_(2) = (-b - √(\Delta))/(2*a)`

`\Delta = b^(2) - 4ac`

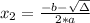
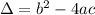
x² + x - 6

Quadratic equation with
`a = 1, b = 1, c = -6`

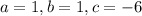
So

`\Delta = 1^(2) - 4(1)(-6) = 25`

`x_(1) = (-1 + √(25))/(2) = 2`

`x_(2) = (-1 - √(25))/(2) = -3`

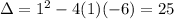
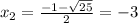
So

`x^2 + x - 6 = (x - 2)(x - (-3)) = (x - 2)(x + 3)`

The complete factorization is:

`-4x(x^2+x-6) = -4x(x - 2)(x + 3)`

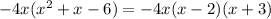
Thus the correct answer is given by option d.