Given:
The equation for the linearized regression line is:
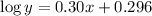
where x represents number of weeks and y be the customer's stock.
To find:
The number of weeks that will pass before the value of the stock reaches $200.
Solution:
We have,
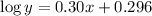
Substituting y=200, we get
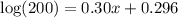
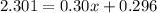
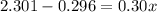

Divide both sides by 0.30.
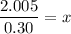
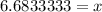
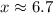
Therefore, the correct option is C.