Question

n a history class there are 88 history majors and 88 non-history majors. 44 students are randomly selected to present a topic. What is the probability that at least 22 of the 44 students selected are non-history majors

Answer 1

0.5675 = 56.75% probability that at least 22 of the 44 students selected are non-history majors.

Explanation:

The students are chosen without replacement from the sample, which means that the hypergeometric distribution is used to solve this question. We are working also with a sample with more than 10 history majors and 10 non-history majors, which mean that the normal approximation can be used to solve this question.

Hypergeometric distribution:

The probability of x successes is given by the following formula:

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

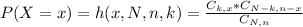
In which:

x is the number of successes.

N is the size of the population.

n is the size of the sample.

k is the total number of desired outcomes.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

Normal Probability Distribution

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

Approximation:

We have to use the mean and the standard deviation of the hypergeometric distribution, that is:

`\mu = (nk)/(N)`

`\sigma = \sqrt{(nk(N-k)(N-n))/(N^2(N-1))}`

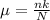
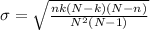
In this question:

88 + 88 = 176 students, which means that
`N = 176`

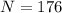
88 non-history majors, which means that
`k = 88`

44 students are selected, which means that
`n = 44`

Mean and standard deviation:

`\mu = (44*88)/(176) = 22`

`\sigma = \sqrt{(44*88*(176-88)*(176-44))/(176^2(175-1))} = 2.88`

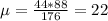
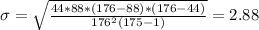
What is the probability that at least 22 of the 44 students selected are non-history majors?

Using continuity correction, as the hypergeometric distribution is discrete and the normal is continuous, this is
`P(X \geq 22 - 0.5) = P(X \geq 21.5)`, which is 1 subtracted by the p-value of Z when X = 21.5. So

`Z = (X - \mu)/(\sigma)`

`Z = (21.5 - 22)/(2.88)`

`Z = -0.17`

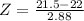
`Z = -0.17` has a p-value of 0.4325

1 - 0.4325 = 0.5675

0.5675 = 56.75% probability that at least 22 of the 44 students selected are non-history majors.