Answer:
The final volume of the sample of gas is 36.287 liters.
Step-by-step explanation:
Let suppose that sample of gas is a closed system, that is, a system with no mass interactions with surroundings, and gas is represented by the equation of state for ideal gases, which is described below:
 (1)
(1)
Where:
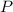 - Pressure, in atmospheres.
- Pressure, in atmospheres.
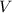 - Volume, in liters.
- Volume, in liters.
 - Molar quantity, in moles.
- Molar quantity, in moles.
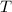 - Temperature, in Kelvin.
- Temperature, in Kelvin.
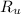 - Ideal gas constant, in atmosphere-liters per mole-Kelvin.
- Ideal gas constant, in atmosphere-liters per mole-Kelvin.
As we know that sample of gas experiments an isobaric process, we can determine the final volume by the following relationship:
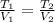 (2)
(2)
Where:
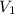 - Initial volume, in liters.
- Initial volume, in liters.
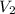 - Final volume, in liters.
- Final volume, in liters.
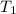 - Initial temperature, in Kelvin.
- Initial temperature, in Kelvin.
 - Final temperature, in Kelvin.
- Final temperature, in Kelvin.
If we know that
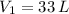 ,
,
 and
and
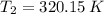 , then the final volume of the gas is:
, then the final volume of the gas is:
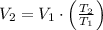


The final volume of the sample of gas is 36.287 liters.