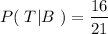Question

a fair coin is flipped. if the flip results in a head, then a fruit is selected from a basket containing 8 apples, 2 bananas, and 6 cantaloups. if the flip results in a tail, then a fruit is selected from a basket containing 6 apples and 4 bananas. what is the probability that the flip resulted in tails, given that the fruit selexted is a banana g

Answer 1

We have given two baskets :

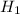`$H_1$` : 8 apples + 2 bananas + 6 cantaloupes = 16 fruits

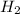`$H_2$` : 6 apples + 4 bananas = 10 fruits

A fair coin is made to flipped. If the
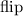`\text{flip}` results is head, then the fruit is selected from a basket
`$H_1$`.

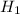If the flip results in tail, then the fruit is selected from the basket
`$H_2$`.

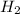Probability of head P(H) =
`1/2`

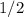
Probability of tail P(T) =
`1/2`

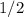
if given event is :

B = selected fruit is BANANA

We have to calculate : P(T|B)

Probability of banana if the flip results is head P(B|H) =
`$(2)/(16)$`

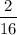
Probability of banana if the flip results is tail P(B|T) =
`$(4)/(10)$`

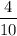
From the Bayes' theorem :

Probability of flip results is tail when selected fruit is BANANA.

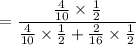
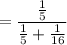
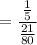
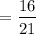
`$P(T|B) = (P(B|T)\ P(T))/(P(B|T) \ P(T) + P(B|H)\ P(H))$`

`$=\frac{(4)/(10) * (1)/(2)} {(4)/(10) * (1)/(2) + (2)/(16) * (1)/(2)}$`

`$=((1)/(5))/((1)/(5)+(1)/(16))$`

`$=((1)/(5))/((21)/(80))$`

`$=(16)/(21)$`

∴
`$P(\ T|B\ )=(16)/(21)$`