Question

Leanne is planning a bridal shower for her best friend. At the party, she wants to serve 33 beverages, 33 appetizers, and 22 desserts, but she does not have time to cook. She can choose from 1313 bottled drinks, 77 frozen appetizers, and 1313 prepared desserts at the supermarket. How many different ways can Leanne pick the food and drinks to serve at the bridal shower

Answer 1

She can pick the food and drinks in 780,780 different ways.

Explanation:

The drinks, appetizers and desserts are independent of each other, so the fundamental counting principle is used.

Also, the order in which the beverages, the appetizers and the desserts are chosen is not important, which means that the combinations formula is used to solve this question.

Fundamental counting principle:

States that if there are p ways to do a thing, and q ways to do another thing, and these two things are independent, there are p*q ways to do both things.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

Beverages:

3 from a set of 13. So

`C_(13,3) = (13!)/(3!10!) = 286`

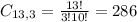
Appetizers:

3 from a set of 7, so:

`C_(7,3) = (7!)/(3!4!) = 35`

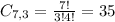
Desserts:

2 from a set of 13, so:

`C_(13,2) = (13!)/(2!11!) = 78`

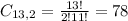
How many different ways can Leanne pick the food and drinks to serve at the bridal shower?

286*35*78 = 780,780

She can pick the food and drinks in 780,780 different ways.