Solution :
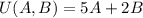
a). Bundles
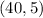 = U ( _____ , 2), lie on the same indifference curve. Suppose missing numbers is x.
= U ( _____ , 2), lie on the same indifference curve. Suppose missing numbers is x.
So,
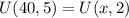
(40 x 5) + (2 x 5) = 50x + (2 x 2)
210 - 4 = 5x
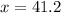
So Alexander has
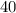 apples and
apples and
 bananas. The indifference curve though
bananas. The indifference curve though
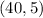 also include bundle.
also include bundle.
Therefore, (41.2, 2)
b).
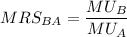
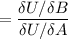

= 0.4
So Alexander has
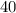 apples and
apples and
 bananas with this bundle. Alexander would like to give up
bananas with this bundle. Alexander would like to give up
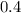 unit apples for a banana.
unit apples for a banana.