Answer:
A
Explanation:
Recall that for a quadratic equation of the form:

The number of solutions it has can be determined using its discriminant:
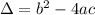
Where:
- If the discriminant is positive, we have two real solutions.
- If the discriminant is negative, we have no real solutions.
- And if the discriminant is zero, we have exactly one solution.
We have the equation:
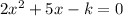
Thus, a = 2, b = 5, and c = -k.
In order for the equation to have exactly one distinct solution, the discriminant must equal zero. Hence:
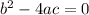
Substitute:
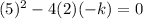
Solve for k. Simplify:

Solve:
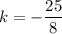
Thus, our answer is indeed A.