The question is incomplete. The complete question is :
A spherical piece of candy is suspended in flowing water. The candy has a density of 1950 kg/m3 and has a 1.0 cm diameter. The water velocity is 1.0 m/s, the water density is assumed to be 1000.0 kg/m3, and the water viscosity is 1.0x10-3 kg/m/s. The diffusion coefficient of the candy solute in water is 2.0x10-9 m2/s, and the solubility of the candy solute in water is 2.0 kg/m3. Calculate the mass transfer coefficient (m/s) and the dissolution rate (kg/s).
Solution :
From flow over sphere, the mass transfer equation can be written as :
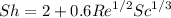
where, Sherood number,
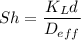
Reynolds number,

Schmid number,
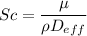
So,

Diameter, d = 1 cm =
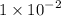 m
m
V = 1 m/s
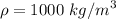
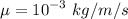
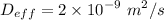

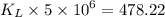
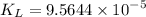 m/s
m/s
So the mass transfer coefficient is 9.5644
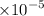 m/s. It is given solubility,
m/s. It is given solubility,
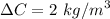
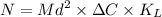
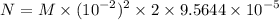
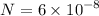 kg/s (dissolution rate)
kg/s (dissolution rate)