Answer:
the average number of cars waiting in line L
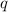 is 0.45
is 0.45
Explanation:
Given the data in the question;
Cars arrive at an automatic car wash system every 10 minutes on average.
Car arrival rate λ = 1 per 10 min = [ 1/10 × 60 ]per hrs = 6 cars per hour
Washing time for each is 6 minutes per car
Car service rate μ = 6min per car = [ 1/6 × 60 ] per hrs = 10 cars per hour
so
P = λ/μ = 6 / 10 = 0.6
Using the length of queue in M/D/1 system since there is only one service bay;
L
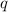 =
=
 [ P² / ( 1 - P ) ]
[ P² / ( 1 - P ) ]
so we substitute
L
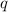 =
=
 [ (0.6)² / ( 1 - 0.6 ) ]
[ (0.6)² / ( 1 - 0.6 ) ]
L
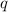 =
=
 [ 0.36 / 0.4 ]
[ 0.36 / 0.4 ]
L
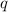 =
=
 [ 0.9 ]
[ 0.9 ]
L
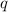 = 0.45
= 0.45
Therefore, the average number of cars waiting in line L
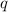 is 0.45
is 0.45