Question

Iron-55 has a half-life of 3 years. How much of a 40 gram sample will remain after 12 years? A. 0 grams B. 4 grams C. 2.5 grams D. 20 grams

Answer 1

`\boxed {\boxed {\sf C. \ 2.5 \ grams }}`

Step-by-step explanation:

We are asked to find how much of a 40 gram sample remains after 12 years.

Iron-55 has a half-life of 3 years. Therefore, after 12 years, 4 half-lives have been completed.

• 12 years/3 years = 4 half-lives

Every time a half-life is completed, half of the sample's mass decays. Remember we start with a 40 gram sample.

• 1 half- life: 40 g / 2 = 20 g
• 2 half-lives: 20 g / 2= 10 g
• 3 half-lives: 10 g / 2 = 5 g
• 4 half-lives: 5 g / 2 = 2.5 g

There is also a formula that can be used to solve this problem.

`A= A_o(\frac {1}{2})^{(t)/(hl)`

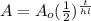
Where A₀ is the initial amount, t is the time, and hl is the half-life.

We know 40 grams is the inital amount, 12 years is the time, and 3 years is the halflife.

• A₀= 40 g
• t= 12
• hl= 3

`A= 40 \ g ((1)/(2))^(12)/(3)`

`A= 40 \ g ((1)/(2))^4`

`A= 40 \ g * 0.0625`

`\bold {A= 2.5 \ g}`

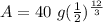
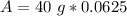
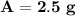
After 12 years, 2.5 grams of Iron-55 will remain.