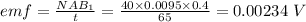Question

A 40-turn coil has a diameter of 11 cm. The coil is placed in a spatially uniform magnetic field of magnitude 0.40 T so that the face of the coil and the magnetic field are perpendicular. Find the magnitude of the emf induced in the coil (in V) if the magnetic field is reduced to zero uniformly in the following times.

(a) 0.30 s V
(b) 3.0 s V
(c) 65 s V

Answer 1

(a) emf = 0.507 V

(b) emf = 0.0507 V

(c) emf = 0.00234 V

Step-by-step explanation:

Given;

number of turns of the coil, N = 40 turns

diameter of the coil, d = 11 cm

radius of the coil, r = 5.5 cm = 0.055 m

magnitude of the magnetic field, B = 0.4 T

The magnitude of the induced emf is calculated as;

`emf = - N(d\phi)/(dt) \\\\where;\\\\\phi \ is \ magnetic \ flux= BA \\\\A \ is the \ area \ of \ the \ coil = \pi r^2 = \pi (0.055)^2 = 0.0095 \ m^2\\\\emf = - N (dB.A)/(dt) = -NA(dB)/(dt) \\\\emf = -NA((B_2 - B_1))/(t) \\\\emf = NA ((B_1 - B_2))/(t) \\\\the \ final \ magnetic \ field \ is \ reduced \ to \ zero;\ B_2 = 0\\\\emf = (NAB_1)/(t)`

(a) when the time, t = 0.3 s

`emf = (NAB_1)/(t) = (40* 0.0095* 0.4)/(0.3) = 0.507 \ V`

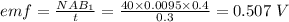
(b) when the time, t = 3.0 s

`emf = (NAB_1)/(t) = (40* 0.0095* 0.4)/(3) = 0.0507 \ V`

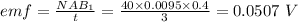
(c) when the time, t = 65 s

`emf = (NAB_1)/(t) = (40* 0.0095* 0.4)/(65) = 0.00234 \ V`