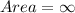Answer:
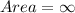
Points of intersection: (1.225,-1.58) and (1.225,1.58)
Explanation:
Given
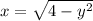
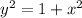
Required
The region area
Plot the graphs of
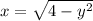 and
and
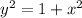
Make y the subject in both equations
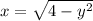
Square both sides
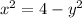
Rewrite
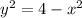
Take square roots
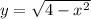
So, we have:
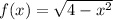
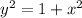
Take square roots
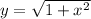
So, we have:
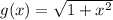
The point of intersection is:
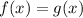
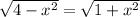
Square both sides
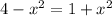
Collect like terms
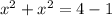
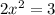
Divide by 2
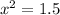
Take square roots
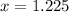
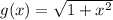
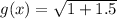
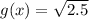
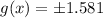
So, the point of intersection is at: (1.225,-1.58) and (1.225,1.58)
See attachment
From the attached image, we can see that the curves do not enclose
Hence: