Answer:
a) R₁ = 14.1 Ω, b) R₂ = 19.9 Ω
Step-by-step explanation:
For this exercise we must use ohm's law remembering that in a series circuit the equivalent resistance is the sum of the resistances
all resistors connected
V = i (R₁ + R₂)
with R₁ connected
V = (i + 0.5) R₁
with R₂ connected
V = (i + 0.25) R₂
We have a system of three equations with three unknowns for which we can solve it
We substitute the last two equations in the first
V = i (
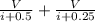 )
)
1 = i (
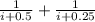 )
)
1 = i (
 ) =
) =
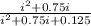
i² + 0.75 i + 0.125 = 2i² + 0.75 i
i² - 0.125 = 0
i = √0.125
i = 0.35355 A
with the second equation we look for R1
R₁ =
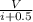
R₁ = 12 /( 0.35355 +0.5)
R₁ = 14.1 Ω
with the third equation we look for R2
R₂ =
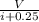
R₂ =
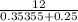
R₂ = 19.9 Ω