Answer:
B
Explanation:
We want to find RX.
Note that RX is adjacent to ∠X and we also know the side opposite to ∠X.
Thus, we can use the tangent ratio. Recall that:
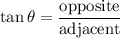
Substitute:
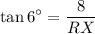
Take the reciprocal of both sides:
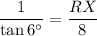
Multiply both sides by 8:
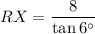
Use a calculator (make sure you're in Degrees mode!):
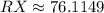
Hence, our answer is B.