Question

A smooth circular hoop with a radius of 0.400 m is placed flat on the floor. A 0.325-kg particle slides around the inside edge of the hoop. The particle is given an initial speed of 8.50 m/s. After one revolution, its speed has dropped to 5.50 m/s because of friction with the floor.

(a) Find the energy transformed from mechanical to internal in the particle "hoop" floor system as a result of friction in one revolution.
(b) What is the total number of revolutions the particle makes before stopping? Assume the friction force remains constant during the entire motion.

Answer 1

a) W = - 6.825 J, b) θ = 1.72 revolution

Step-by-step explanation:

a) In this exercise the work of the friction force is negative and is equal to the variation of the kinetic energy of the particle

W = ΔK

W = K_f - K₀

W = ½ m v_f² - ½ m v₀²

W = ½ 0.325 (5.5² - 8.5²)

W = - 6.825 J

b) find us the coefficient of friction

Let's use Newton's second law

fr = μ N

y-axis (vertical) N-W = 0

fr = μ W

work is defined by

W = F d

the distance traveled in a revolution is

d₀ = 2π r

W = μ mg d₀ = -6.825

μ =
`( -6.825)/(d_o \ mg)`

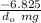
The total work as the object stops the final velocity is zero v_f = 0

W = 0 - ½ m v₀²

W = - ½ 0.325 8.5²

W = - 11.74 J

μ mg d = -11.74

we subtitle the friction coefficient value

(
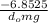`(-6.8525 )/(d_o mg)`) m g d = -11.74

6.825
`(d)/(d_o)` = 11.74

d = 11.74/6.825 d₀

d = 1.7201 2π 0.400

d = 4.32 m

this is the total distance traveled, the distance and the angle are related

θ = d / r

θ = 4.32 / 0.40

θ = 10.808 rad

we reduce to revolutions

θ = 10.808 rad (1rev / 2π rad)

θ = 1.72 revolution