Question

HELPPPPP

A geometric series has three terms. The sum of the three terms is 42. The third term is 3.2 times the sum of the other two. What are the terms?

Answer is : 2,8, and 32
Please show steps because I'm very confused

Answer 1

Explanation:

A geometric series means that we multiply one number by a common ratio to get the second number. Let's say our first number is x, and our common ratio is y. We can write the first term is x, and to get the second number, we multiply x by our common ratio, y. For example, if 5 was the first number and 2 was the common ratio, the second number would be 5*2 = 10, and the third would be 10 * 2 = 20.

For our question, the first number is x, the second is x*y, and the third is x*y*y = x*y²

The sum of these three terms is 42, so we can say

x + x*y + x*y² = 42

Next, the third term is equal to 3.2 times the sum of the other two. First, we have 3.2 times something. That something is the sum of the other two, so we must prioritize calculating the sum of the first two numbers, and then multiply that by 3.2 to get the third. We can write this as

(x + x*y) * 3.2 = x*y²

factor out x

x * 3.2(1 +y) = x*y²

divide both sides by x

3.2(1+y) = y²

expand

3.2 + 3.2y = y²

subtract (3.2 + 3.2y) from both sides to make this a quadratic equation

y²-3.2y-3.2 = 0

use the quadratic formula to solve for y (note that +- here stands for "plus or minus")

`y = \frac{-(-3.2) +- \sqrt{3.2^(2)-4(-3.2)(1)} }{2} \\= (3.2+-√(10.24+12.8) )/(2) \\= (3.2+- 4.8)/(2)`

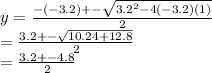
= -0.8 or 4

With these two possibilities, we can try each in our other equation to see what works.

x + x*y + x*y² = 42

for y = -0.8

x + -0.8x + 0.64x = 42

x - 0.16x = 42

0.84x = 42

multiply both sides by 1/0.84 to isolate the x

x=50

This works, with x (the first number) =50, the second number being 50 * -0.8 = -40, and the third being -40 * -0.8 = 32. 50+(-40) = 10, 10*3.2=32, and 50-40+32 = 42

Next, for y=4, we have

x+4x + 16x= 42

21x = 42

divide both sides by 21 to isolate the x

This works as well, with x=2, the second value being 2*4 = 8, and the third value being 8*4 =32. 2+8=10, 10*3.2 = 32, and 2+8+32 = 42

Answer 2

Let x be the first term in the geometric sequence. Then the next two terms in the sequence are xr and xr ², where r is some constant. (This is the defining characteristic of geometric sequences.)

The sum of the first three terms is 42, so

x + xr + xr ² = 42

x (1 + r + r ²) = 42

The third term is 3.2 times the sum of the other two, so that

xr ² = 3.2 (x + xr )

Solve the second equation for r :

xr ² = 3.2 x (1 + r )

We can divide both sides by x since x ≠ 0. (This is obvious, since if x was zero, then all three terms in the sequence would be 0.)

r ² = 3.2 (1 + r )

r ² = 3.2 + 3.2r

r ² - 3.2r - 3.2 = 0

r ² - 16/5 r - 16/5 = 0

5r ² - 16r - 16 = 0

(5r + 4) (r - 4) = 0

==> r = -4/5 or r = 4

Since there are two possible values of r that might work, there are two possible sequences that meet the criteria.

Plug either of these solutions into the first equation:

r = -4/5 ==> x (1 + (-4/5) + (-4/5)²) = 42

… … … … … … 21/25 x = 42

… … … … … … x = 50

r = 4 ==> x (1 + 4 + 4²) = 42

… … … … … 21x = 42

… … … … … x = 2

Then the two possible answers would be

• if r = -4/5, then the three terms are {50, -40, 32}

• if r = 4, then they are {2, 8, 32}