Answer: Attached below is the well written question and solution
answer:
i) Attached below
ii) similar parameter =
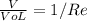
Step-by-step explanation:
Using ; L as characteristic length and Vo as reference velocity
i) Nondimensionalize the equations
ii) Identifying similarity parameters
the similar parameters are =
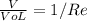
Attached below is the detailed solution